Public transport networks of towns and districts are characterized by the available transport systems, routes and frequencies of lines, time tables, and fares. These characteristics are designed in a planning step called strategic planning. It involves challenging optimization problems that include multiple objectives, feedback effects on the demand, and complex technical, administrative, and regulatory requirements. The goal of this project is to develop a mathematical optimization toolbox for strategic planning problems to be used for decision support. So far, we concentrated on line and fare planning in public transport. We have developed new mathematical optimization models and algorithms for these problems.
Line Planning
In line planning, the task is to design lines (paths and frequencies) in a given network such that the demand (given by an origin-destination matrix) can be served. The objective tries to find a compromise between quality and cost. We developed a path-based multi-commodity flow model, which links passenger flows and line routes. It includes features that have not been considered before in this context, namely, dynamic generation of lines and free routing of passengers according to the computed lines. The literature mainly deals with line planning for railways. In these approaches, passenger paths are fixed a priori using a concept called system-split and lines are chosen from a precomputed line pool.
Our mathematical results analyze the complexity of the model: Solving the LP relaxation is NP-hard, pricing the passenger paths can be done in polynomial time, while line pricing is an NP-hard longest path problem. However, we proved that the case of logarithmic line lengths can be solved in polynomial time using a derandomized coloring approach.
On the algorithmic side, we developed a column generation method using an exact search for line paths. Our implementation can compute the optimal solution of the LP relaxations of line planning problems for the entire public transport network of Potsdam (with 410 nodes and 891 edges) in less than one hour. These instances are substantially larger and more complex than the networks considered in the literature.
We are currently working on methods to construct high-quality integer solutions for the line planning problem. We are in regular exchange with our cooperation partners ViP Potsdam GmbH and IVU Traffic Technologies AG in order to assess the practical feasibility of our line plans.
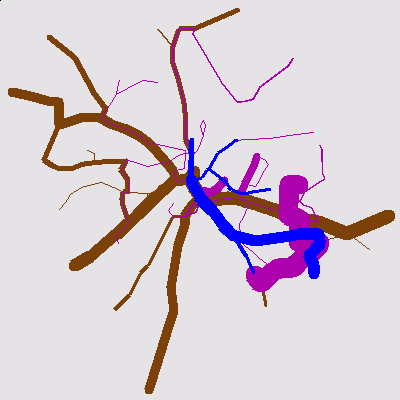 | 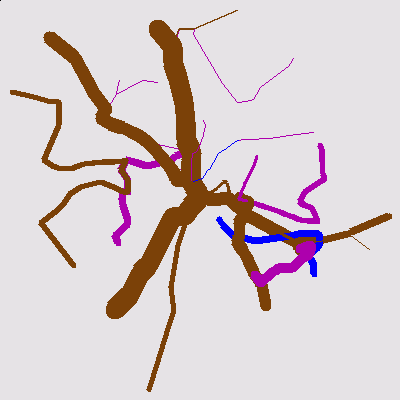 |
| Old lines in Potsdam | Computed lines |
| Pictures produced with JavaView (Project F4) | |
Example: On the left picture above, you can see the existing lines of Potsdam in 1998. The thickness of the edges is proportional to the frequency of the lines. The following color-coding is used: Blue = tram, Violet = city-bus, brown = regional bus. The transportation systems train, city railroad, and ferry are not shown since they are not operated by our cooperation partners. The right picture shows the result of our optimization.
Fare Planning
In fare planning, the task is to design a system of fares for different ticket types in order to maximize the revenue of a public transportation company. For instance, a ticket might include a basic fare and a distance dependent fare (e.g. the German Bahn-Card). These fares affect the passenger demands between different points in the network, which in turn determines the revenue. As far as we know, no optimization approach to this type of fare planning has appeared in the literature before. We developed a novel nonlinear optimization model based on logit-type discrete choice demand functions (Borndörfer, Neumann, and Pfetsch 2005). Applying standard software we computed optimal fares for the Dutch intercity network, involving several public transport ticket types and the alternative to use a car.
Example: There are three alternatives: standard ticket, reduced ticket, and car. For a standard ticket one has to pay a distance dependent fare (x-axis/Euro). To use a reduced ticket one has to pay a basic fare (y-axis/Euro) and then a 50% reduced distance dependent fare. The price to use a car involves a basic fare of 100 Euro and a distance dependent price of 0.1 Euro/km. The revenue function resulting from our model can be seen in the figures below.
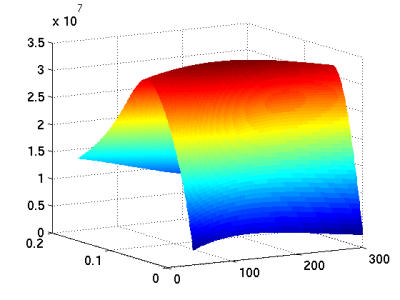 | 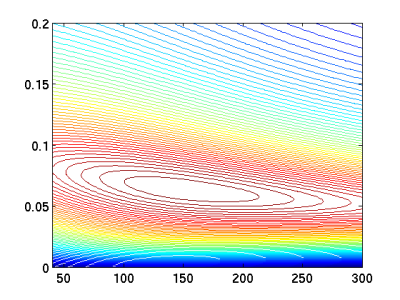 |
| Revenue function obtained from our discrete choice model | Contour plot of revenue function |
Poster [pdf]